《三体》电视剧热播,关于“三体问题为什么无解”的搜索量也开始飙升。
很多小伙伴认为这是一个非常反直觉的结论,“三体问题”无非就是求解三个质点在万有引力作用下的运动轨迹,它的描述如此简单,怎么会不可解呢?就算不能用数学公式给出一个解析形式的通解,为什么得到一个长期的数值解(即电视剧中的“万年历”)也这么难呢?
简单来说,三体问题的解析解需要解出一组微分方程,我们现在只能找到有限的特例,不能得出通解。而三体问题的数值解,是一个“混沌”问题,数值条件上的任何细微改变,都会引起结果的巨大变化,导致无法做出长期的准确预测。
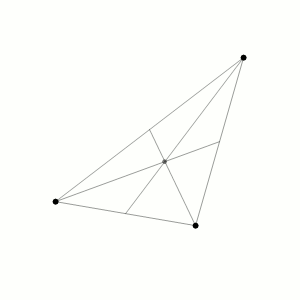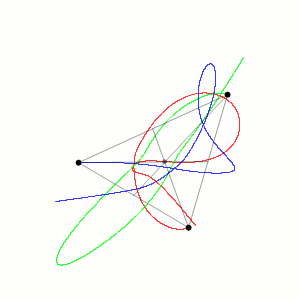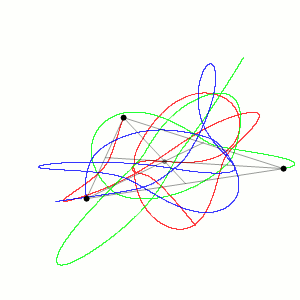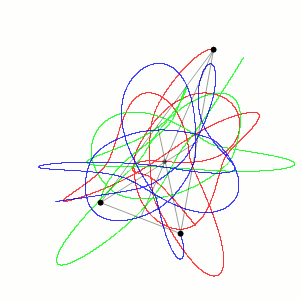
我们熟悉的“蝴蝶效应”就是混沌的例子:南美洲的一只蝴蝶扇动翅膀,最终会在佛罗里达引起一场飓风。就像令人伤脑筋的数值天气预报,明天的天气预报相对靠谱,但15天的天气预报就很不准了。
说到这里,可能还是让人觉得不服气,混沌有什么难算的,我们不是有计算机吗?那么,我来带你手算一个混沌序列感受一下吧,可以使用Excel或WPS表格来做。
计算公式非常简单:
xn+1=4xn(1-xn)
把这个序列放进Excel,给一个0~1之间的初始值,比如0.3吧。然后做另一个同样的序列,只把初始值的小数点后第六位稍微改动一下,变成0.300001。画图看看这两个序列:
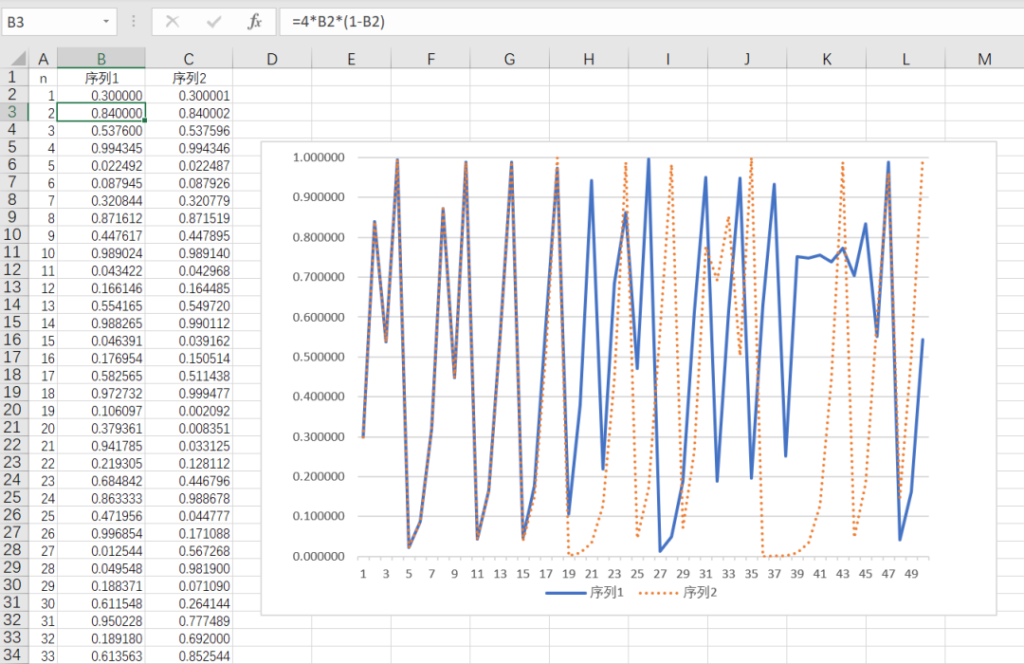
可以看到,差不多迭代20次之后,两个序列就开始分道扬镳,正所谓“失之毫厘,谬以千里”。你看,上面的计算仅仅是小数点后6位差了一点,就足以让预测误差在20次之内肉眼可见。
计算机的精度总是有限的。如果我们想从第1个元素开始,预测出第10000个元素,那么在中间就会因为精度丢失的问题出现无法避免的误差,导致整个序列的预测越来越不准确。也就是说,混沌序列只能在有限的范围内给出预测。万年历?办不到啊。
随便来一个迭代500次的混沌序列看看,乱就一个字:
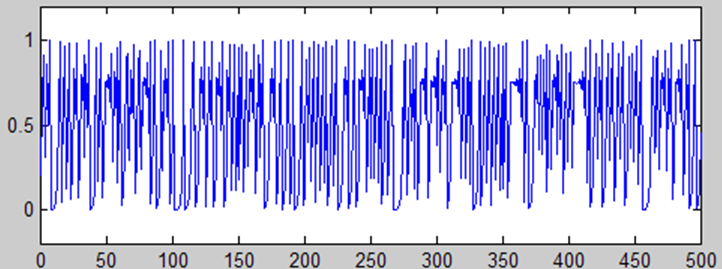
如此简单的一个初等数学数列都会因为细微扰动出现混沌现象,那么三体问题的数值解出现混沌状态也就不难理解了。
类似的混沌问题有很多,双摆也是一例,初始条件稍有不同的双摆,很快就会呈现完全不同的运动轨迹:

混沌看似混乱、随机,但也有一些有趣的应用。例如混沌序列就可以用在加密上。如果把混沌序列的初始值作为密码,在计算方法和计算精度一样的条件下,就可以用一个初始值生成一组任意长的、规律难以推测的序列,这个序列就可以用来加密。我们把这样可以算出、但看似随机的序列称为“伪随机序列”。
例如我曾经做过的图像加密算法,它的作用是把一个图像的像素重新排列,变成这样:

算法伪码:
获取由六位数字组成的用户密码x;
使用线性映射将用户密码x变为一个0~1之间的初始值;
设图像块总数为L,迭代前述混沌序列,得到长度为L的混沌序列N;
将N做降序排列,得到排序置换向量S;
利用向量S重排各个图像块。
- 显然,这个算法是可逆的,用同样的密码逆操作就可以把杂乱无章的像素还原出原图。
伪随机序列的另一个著名应用是移动通信中的CDMA技术,原理与上面的图像加密是类似的,这里就不展开了。
本文用爱因斯坦的话来结尾最为合适:
宇宙的永恒之谜在于其可理解性,宇宙能被理解是个奇迹。The most incomprehensible thing about the Universe is that it is comprehensible.
(Albert Einstein, 1936)
以及冯诺依曼的断言:
任何人如果相信计算机能够产生出真正的随机的数序组,都是疯了。Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.
(John von Neumann, 1951)
以上。
做中学的老狼
